Problem
ASSA ABLOY SA is a company specializing in door opening solutions. One part of the company focuses on manufacturing pin tumbler and lever locks for multiple brands including Union, Yale and Multi-Lock. The production line used to produce padlocks is a perfect example of a network system; the steps are shown in Table 1. Using this example, the CPM (critical path method) will be explained fully.
For the purpose of the example, a batch of 200 padlocks will be taken as the sample for the data recorded.
Table 1: Steps followed to produce padlocks.
For the purpose of the example, a batch of 200 padlocks will be taken as the sample for the data recorded.
Table 1: Steps followed to produce padlocks.
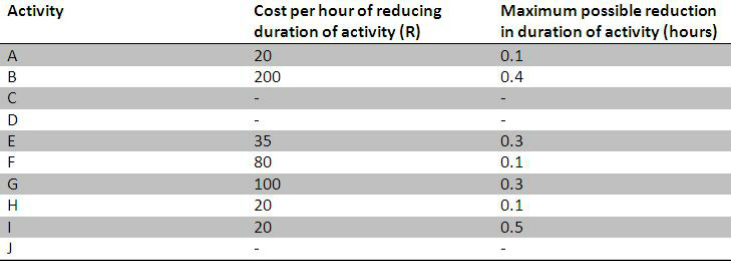
Extra costs are associated with the activities if the manager wants to reduce the overall time (or critical path). These costs can be seen from table 2, as well as the maximum reduction in time per activity.
Table 2: Costs of making reductions in the duration of the activities.
Table 2: Costs of making reductions in the duration of the activities.
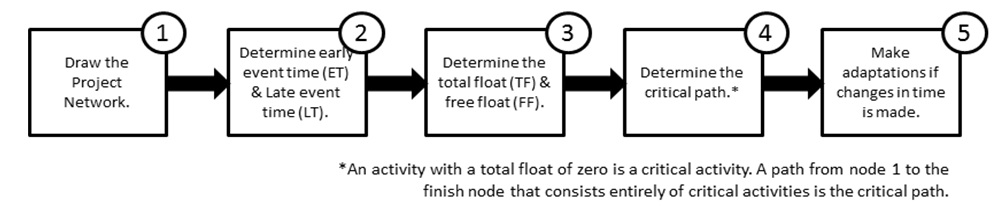
CPM Explained
The CPM will be explained using the above example to develop a basic understanding of the steps involved.
The CPM will be explained using the above example to develop a basic understanding of the steps involved.
Figure 1: Process of CPM
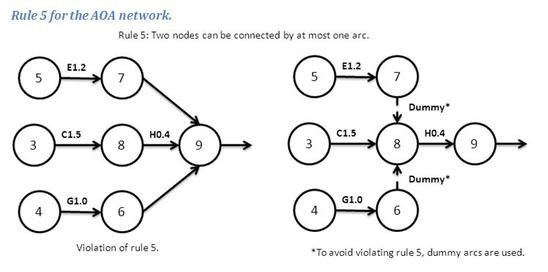
Figure 2: Demonstration of the use of dummies
Solving the problem (by hand)
1. Drawing the Project Network
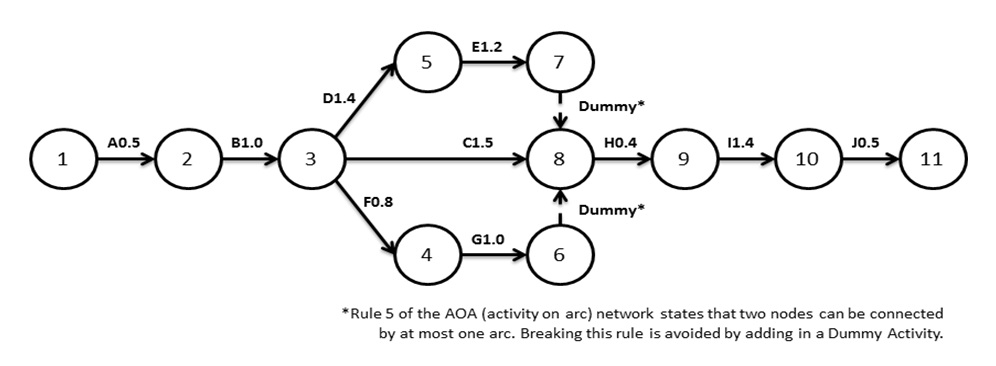
The first step of the CPM is to draw the project network. The steps are shown below:
Figure 3: The process for drawing the activity on arc (AOA) network.
Figure 4: ASSA ABLOY's process for manufacturing padlocks.
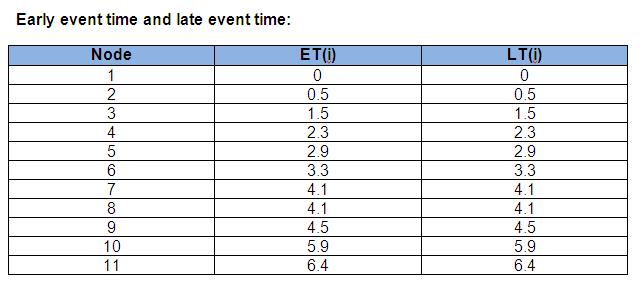
2. Determining early event time (ET) and late event time (LT)
ET(1) = 0
ET(2) = ET(1) + 0.5 = 0.5
ET(3) = ET(2) + 1 = 1.5
ET(4) = ET(3) + 0.8 = 2.3
ET(5) = ET(3) + 1.4 = 2.9
ET(6) = ET(4) + 1 = 3.3
ET(7) = ET(5) + 1.2 = 4.1
ET(6) + 0 = 3.3
ET(8) = max between : ET(3) + 1.5 = 3
ET(7) + 0 = 4.1
ET(9) = ET(8) + 0.4 = 4.5
ET(10) = ET(9) + 1.4 = 5.9
ET(11) = ET(10) + 0.5 = 6.4 (Longest time to complete activities)
2. Determining early event time (ET) and late event time (LT)
ET(1) = 0
ET(2) = ET(1) + 0.5 = 0.5
ET(3) = ET(2) + 1 = 1.5
ET(4) = ET(3) + 0.8 = 2.3
ET(5) = ET(3) + 1.4 = 2.9
ET(6) = ET(4) + 1 = 3.3
ET(7) = ET(5) + 1.2 = 4.1
ET(6) + 0 = 3.3
ET(8) = max between : ET(3) + 1.5 = 3
ET(7) + 0 = 4.1
ET(9) = ET(8) + 0.4 = 4.5
ET(10) = ET(9) + 1.4 = 5.9
ET(11) = ET(10) + 0.5 = 6.4 (Longest time to complete activities)
Figure 5: Early event time and late event time for given problem
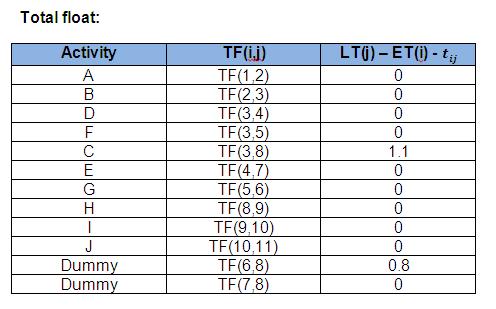
3. Determining the total float (TF) and free float (FF)
3. Determining the total float (TF) and free float (FF)
Figure 6: Determining the total float
Figure 7: Determining the free float
4. Determine the critical path
The critical path in any project network is the longest path from the start node to the finish node.
· An activity with a total float of zero is a critical activity.
· A path from node 1 to the finish node that consists entirely of critical activities is the critical path.
As can be seen from above, the critical path is: 1 – 2 – 3 – 5 – 7 – 8 – 9 – 10 – 11
Linear Programming application
In the above formula represents the time assigned to the arc connecting activity with activity . By setting one ensures that the preceding activity is completed first.
Objective function: min z = x11 - x1
Subject to: x2 >= x1 + 0.5 (arc(1,2) constraint)
x3 >= x2 + 1 (arc(2,3) constraint)
x4 >= x3 + 0.8 (arc(3,4) constraint)
x5 >= x3 + 1.4 (arc(3,5) constraint)
x6 >= x4 +1 (arc(4,6) constraint)
x7 >= x5 +1.2 (arc(5,7) constraint)
x8 >= x3 + 1.5 (arc(3,8) constraint)
x9 >= x8 + 0.4 (arc(8,9) constraint)
x10 >= x9 + 1.4 (arc(9,10) constraint)
x11 >= x10 + 0.5 (arc(10,11) constraint)
x8 >= x7 (dummy arc(7,8) constraint)
x8 >= x6 (dummy arc(6,8) constraint)
All variable urs
5. Crashing the project
When the time of an activity can be reduced at an additional cost a different LP needs to be taken into consideration. This usually occurs when a project needs to be completed in a time shorter than the current critical path. For the ASSA ABLOY example the following will happen:
A = the time reduction for the first activity.
……
J = the time reduction for the last activity.
To determine the minimum cost the following LP will need to be solved. Also assume that the path time required is 6.3 hours.
Objective function: min z = 20A + 200B + 0C + 0D + 35E + 80F + 100G + 20H + 20I + 0J
Subject to: A <= 0.1
B <= 0.4
C <= 0
D <= 0
E <= 0.3
F <= 0.1
G <= 0.3
H <= 0.1
I <= 0.5
J <= 0
x2 >= x1 + 0.5 - A (arc(1,2) constraint)
x3 >= x2 + 1 - B (arc(2,3) constraint)
x4 >= x3 + 0.8 - F (arc(3,4) constraint)
x5 >= x3 + 1.4 - D (arc(3,5) constraint)
x6 >= x4 + 1 - G (arc(4,6) constraint)
x7 >= x5 +1.2 - E (arc(5,7) constraint)
x8 >= x3 + 1.5 - C (arc(3,8) constraint)
x9 >= x8 + 0.4 - H (arc(8,9) constraint)
x10 >= x9 + 1.4 - I (arc(9,10) constraint)
x11 >= x10 + 0.5 - J (arc(10,11) constraint)
x8 >= x6 (dummy arc(6,8) constraint)
x8 >= x7 (dummy arc(7,8) constraint)
x11 - x1 <= 6.3 (time constraint)
A, B, C, D, E, F, G, H, I, J >= 0
xi urs
The first 10 constraints are for the reduction in time for each activity.
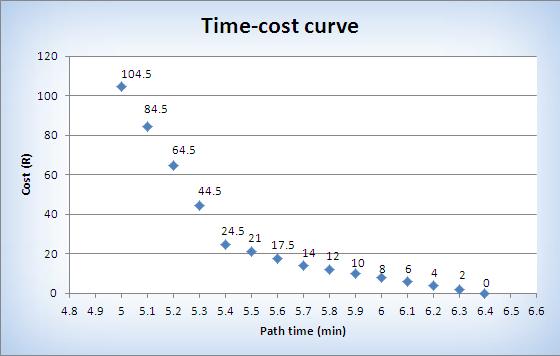
As can be seen from the graph below, the cost increases exponentially as the path time decreases.
The critical path in any project network is the longest path from the start node to the finish node.
· An activity with a total float of zero is a critical activity.
· A path from node 1 to the finish node that consists entirely of critical activities is the critical path.
As can be seen from above, the critical path is: 1 – 2 – 3 – 5 – 7 – 8 – 9 – 10 – 11
Linear Programming application
In the above formula represents the time assigned to the arc connecting activity with activity . By setting one ensures that the preceding activity is completed first.
Objective function: min z = x11 - x1
Subject to: x2 >= x1 + 0.5 (arc(1,2) constraint)
x3 >= x2 + 1 (arc(2,3) constraint)
x4 >= x3 + 0.8 (arc(3,4) constraint)
x5 >= x3 + 1.4 (arc(3,5) constraint)
x6 >= x4 +1 (arc(4,6) constraint)
x7 >= x5 +1.2 (arc(5,7) constraint)
x8 >= x3 + 1.5 (arc(3,8) constraint)
x9 >= x8 + 0.4 (arc(8,9) constraint)
x10 >= x9 + 1.4 (arc(9,10) constraint)
x11 >= x10 + 0.5 (arc(10,11) constraint)
x8 >= x7 (dummy arc(7,8) constraint)
x8 >= x6 (dummy arc(6,8) constraint)
All variable urs
5. Crashing the project
When the time of an activity can be reduced at an additional cost a different LP needs to be taken into consideration. This usually occurs when a project needs to be completed in a time shorter than the current critical path. For the ASSA ABLOY example the following will happen:
A = the time reduction for the first activity.
……
J = the time reduction for the last activity.
To determine the minimum cost the following LP will need to be solved. Also assume that the path time required is 6.3 hours.
Objective function: min z = 20A + 200B + 0C + 0D + 35E + 80F + 100G + 20H + 20I + 0J
Subject to: A <= 0.1
B <= 0.4
C <= 0
D <= 0
E <= 0.3
F <= 0.1
G <= 0.3
H <= 0.1
I <= 0.5
J <= 0
x2 >= x1 + 0.5 - A (arc(1,2) constraint)
x3 >= x2 + 1 - B (arc(2,3) constraint)
x4 >= x3 + 0.8 - F (arc(3,4) constraint)
x5 >= x3 + 1.4 - D (arc(3,5) constraint)
x6 >= x4 + 1 - G (arc(4,6) constraint)
x7 >= x5 +1.2 - E (arc(5,7) constraint)
x8 >= x3 + 1.5 - C (arc(3,8) constraint)
x9 >= x8 + 0.4 - H (arc(8,9) constraint)
x10 >= x9 + 1.4 - I (arc(9,10) constraint)
x11 >= x10 + 0.5 - J (arc(10,11) constraint)
x8 >= x6 (dummy arc(6,8) constraint)
x8 >= x7 (dummy arc(7,8) constraint)
x11 - x1 <= 6.3 (time constraint)
A, B, C, D, E, F, G, H, I, J >= 0
xi urs
The first 10 constraints are for the reduction in time for each activity.
As can be seen from the graph below, the cost increases exponentially as the path time decreases.
Graph 1: Cost and path time relationship